Developed by the Statistician Ronald Fisher, Analysis of Variance (ANOVA) is a statistical model that helps to us to analyse the variability present in the data.
Analysis of Variance (ANOVA) – One Way: The total variation present in a set of observable quantities may under certain circumstances be partitioned into a number of disjoint components associated with the nature of the classification of the data. So, this systematic methodology by which one can partition the causes of variation into several components is called Analysis of Variance.
Let us consider an example of yield of paddy. Suppose the yield is carried out using three kinds of seeds. So, the yield variation occurs due to variation of seed and also due to some random error (the position of seed was suitable for germination). This is a classic example of one-way layout of ANOVA.
Assumptions
- The observations recorded were independent
- Parent population from which observations were taken have Normal distribution.
- Homogeneity of variances in the different treatment groups i.e. the variance of all the treatment groups is equal.
One way ANOVA
The main theory behind Completely Randomized Design (CRD) is One-way ANOVA.
Let us consider the following Example.
A spots analyst was curious. He wanted to know that if the physical weight of players differs due to different training strategies of 5 different clubs. For this purpose, he gathered 5 groups from each of the 5 clubs.
Theory
Here the weight of a player is influenced by a single treatments/Factor, Club, A and the factor has 5 levels.
A(Factor): Clubs from which a professional football player plays for.
First Level (Cowboys): players from the Dallas Cowboys
Second Level (Packers): players from the Green Bay Packers
Third Level (Broncos): players from the Denver Broncos
Fourth Level (Dolphins): players from the Miami Dolphins
Fifth Level (Niners): players from the San Francisco Forty Niners
So, there are 5 treatments and ith treatment (where i=1,2,3,4,5) is replicated ri =17 times. To clarify, it can be looked upon as a similar setup like ANOVA one way fixed-effect model, where a single factor has 5-levels and each level consists of ri =17observations.
For ith level, let there be ni observations,
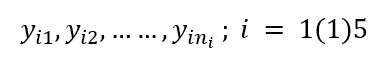
We represent the observations in the following array data.
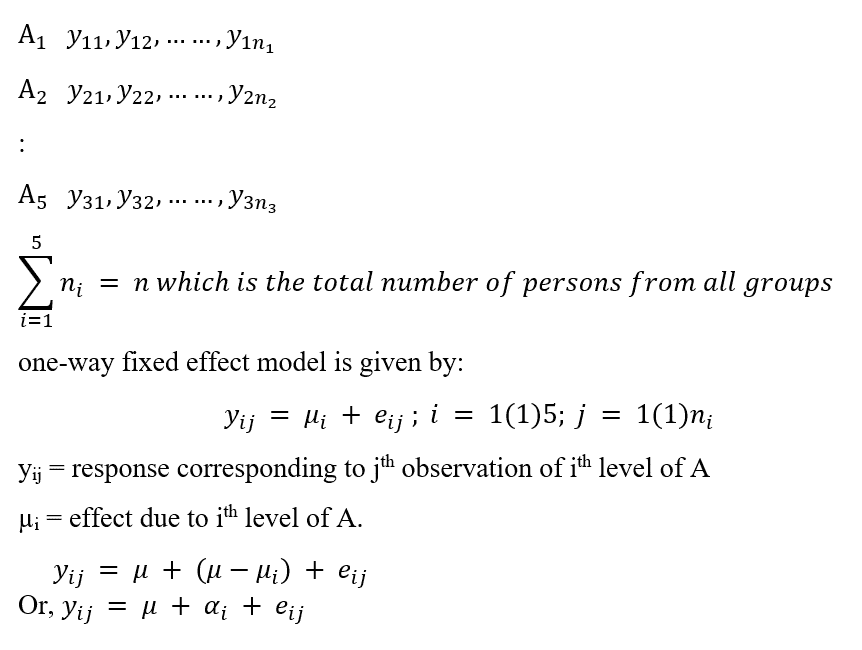

Analysis of Variance (ANOVA) – One Way using R
Code:
Note: Do not choose Excel formal for this case because it doesn’t read the levels of a factor.
Consider the following code and output for illustration:
player_weight <- read_excel("E:/mathematicacity/player weight.xlsx"
col_types = c("numeric", "text"))
View(player_weight)
[1] "Weight" "Club"
levels(player_weight$Club)
Note that R cannot read its levels. (giving output as NULL)]
#Choosing dataset (if the dataset is in .csv Format my_data <- read.csv(file.choose()) View(my_data) Preview of the data:
| Weight | Club |
| 250 | Cowboys |
| 255 | Cowboys |
| 255 | Cowboys |
| 264 | Cowboys |
| 250 | Cowboys |
| 265 | Cowboys |
71 more columns
# Show the levels names(my_data) levels(my_data$Club) Output: [1] "Weight" "Club" [1] "Broncos" "Cowboys" "Dolphins" "Niners" [5] "Packers"
#Estimation of Model model1 <- aov(Weight ~ Club, data = my_data) summary(model1)
| Df | Sum sq. | Mean Sq. | F value | Pr(>F) | |
| Club | 4 | 1714 | 428.4 | 1.575 | 0.189 |
| Residuals | 80 | 21761 | 272.0 |
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The output includes the columns F value and Pr(>F) corresponding to the p-value of the test. From the p-value we cannot reject the Null Hypothesis at 5% level of Significance.
So, we can conclude that at 5% level of Significance the physical weight of plyers does not differ significantly due to different training strategies of 5 different clubs.
[Note: But if the Null hypothesis was rejected then we can perform a paired comparison with the help of Tukey test and can find out which club’s training strategy differs significantly. The R code for this is:TukeyHSD(model1, conf.level = 0.95)
We will consider an example in the Next portion of 2-way ANOVA so that we can perform the Tukey test.]
Checking Assumptions of ANOVA
##Checking ANOVA assumptions
# 1. Homogenity of variances
install.packages("car")
library(car)
leveneTest(Weight ~ Club, data = my_data)
Output:
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 4 0.0956 0.9836
80
From the output above we can see that the p-value is not less than the significance level of 0.05. Moreover, this means that there is no evidence to suggest that the variance across groups is statistically significantly different. Therefore, we can assume the homogeneity of variances in the different treatment groups.
# 2. Normality plot(model1, 2) # Extract the residuals aov_residuals <- resid(model1 ) # Run Shapiro-Wilk test shapiro.test(x = aov_residuals ) Output:
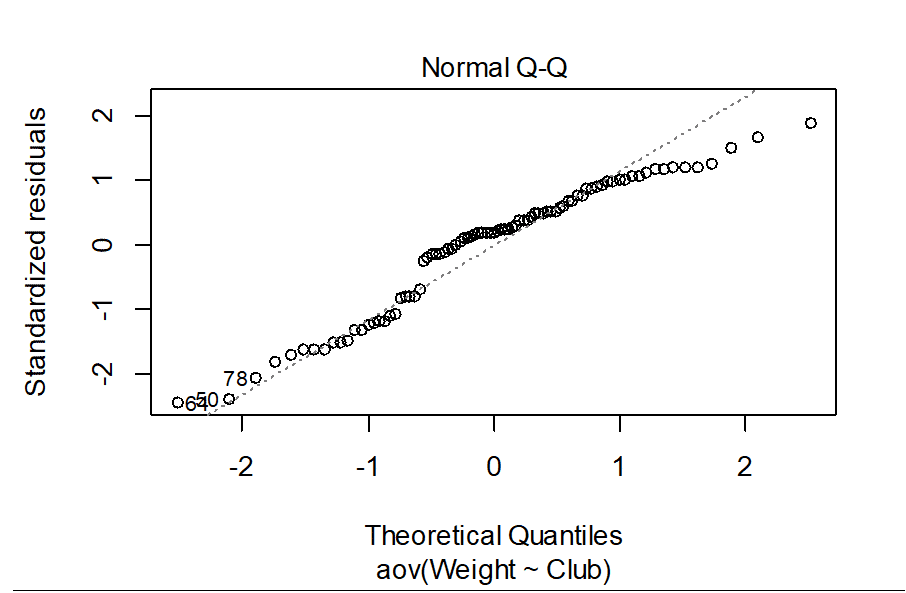
data: aov_residuals
W = 0.94462, p-value = 0.001161
So, from the p-value and the plot, we can see that the data does not violate the Normality assumption of ANOVA.
I hope this article was helpful and now you’d be comfortable in solving similar problems using Analysis of Variance.
This article was written by Shreyansh Agarwal and Kountenyo Roy Chowdhury.
For more such articles visit The Actuarial Club.
This article was published by Kautilya Sharma.

