In this article, I will be talking about how to build a Multi-Variate Time Series Modelling – Vector Auto Regressive (VAR) Model in R. I will be exploring the available dataset, how to decide upon certain factors which affects the model, execution and comparison between the actual v/s predicted values.
What is VAR?
Vector Auto-regression (VAR) is a stochastic process model useful when one is interested in predicting multiple time series variables using a single model. It is an extension of univariate Autoregressive (AR) model. The general notation is:
VAR(1):

Each variable in the model has one equation. The current (time t) observation of each variable depends on its own lagged values as well as on the lagged values of each other variable in the VAR. For detailed theoretical information, check out this link.
Data Description:
The data for this model is taken from Federal Reserve Bank of St. Louis. Here my objective is to predict the GDP of USA by taking into account not only past GDP numbers but also using some of its components: Gross Domestic Private Investment (GDPI), Exports (EX) and Imports (IM). The data was from 1999 to 2019 as stated quarterly (in billions of dollars).
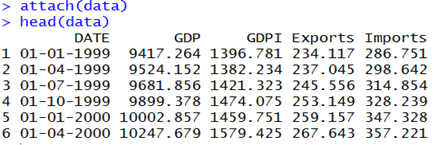
Generally, in time series modelling we need to divide the dataset manually in order to visualize actual v/s predicted. So, I have built the model using data from 1999 to 2017 and tried to predict and compare the GDP values for the years 2018-2020.
Data Exploration:
For multi-variate time series modelling, I will be using various built-in packages in R: forcast, vars, tseries, urca and xlsx. Before starting off with any model we should always keep in mind to explore and understand the available data and the find any reasons for abnormality if any.
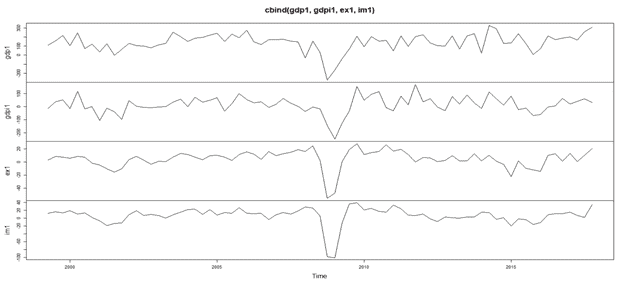
After importing the data and converting it to a time series, here is combined plot of all the variables:
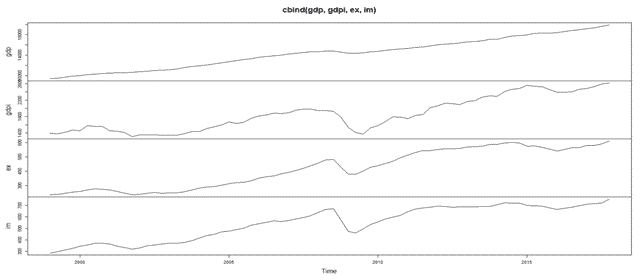
We can clearly see that we have an upward trend with a dip around the year 2008 for all the variables. It was due to the economic crisis of 2008 which led to the dent of US economy. We can observe that the data is not stationary due to the trend.
Stationarity and Differencing of Data:
We will check with the Augmented Dickey-Fuller (ADF) Test to look whether we need to difference the data for achieving stationarity. The results are as follows:
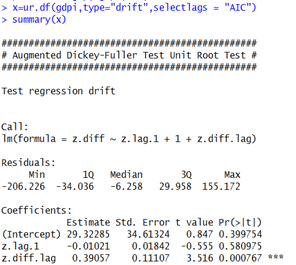
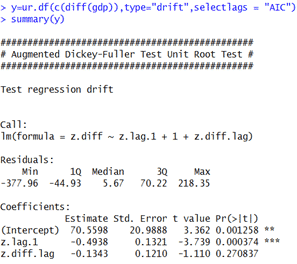
Here the Ho is the data is stationary whereas H1 is the data is not stationary. We can see that when the data is differenced once the p value is below the threshold of 5% and we can accept Ho. We can also see by plotting the differenced data that the data seems to be stationary:
By looking at these results, theoretically we should continue with using the differenced data. But here since we are building VAR model, we do not have differencing (d) factor as in ARIMA model. So we will be using the actual stated data in the model even if it is not stationary. Also while running this model one should always keep in mind that whenever we have some stated values (like GDP) we should not difference the data and proceed with VAR.
Which lag to choose?
For choosing the lag (p) of the model we will use VARselect command to look at best possible lag under different criteria. Here I will be checking which lag to choose by keeping the maximum limit upto 10 lags:

The four types of selection criterion are as follows:
- Akaike Information Criterion (AIC)
- Hannan-Quinn Criterion (HQ)
- Schwarz-Bayes Criterion/Bayesian Information Criterion (SC or BIC)
- Final Prediction Error Criterion(FPE)
For more information on these you can click to this link. The widely used criterion to select the lag is AIC and BIC which suggests using 10 and 2 lags respectively.
Before choosing any recommended lag we should again keep in mind the practical and logical sense of using that lag. Here using a lag of 10 means that the present predictions will depend upon the past 2.5 years of data which seemed a little illogical given the fact that in 2.5 years the economic factors of a country could change drastically. Whereas using a lag of 2 (past 6 months) looks ideal. For our better understanding I will be executing the model using both the lags to compare the results and interpret how these different lags leads to different predictions.
Execution:
After choosing the lag, with the help of VAR command we will run our model. We will have a look at the summary of the model with lag 2 and you can try out the codes to observe how the model with lag 10 is performing.

By default we input “type=const” and since we do not have any dummy season variable or any other exogenous variables, we will simply state NULL for them. Here, we are only displaying the equation for GDP due to space crunch but the model gives us the equation for all the input variables. Have a look at them as well for better understanding of the model.
After looking at the adjusted R squared value of 0.9992 we can interpret that the model’s performance is excellent. The * mark beside the variables shows us that they are statistically significant to the model.
Ganger- Causality Test:
Granger causality test is a way to investigate causality between two variables in a time series i.e. whether a variable X is causal to variable Y (if X is the cause of Y/ Y is the cause of X). Ideally, we should have some relationship between the variables for running VAR model. Otherwise the model might not be robust and results may be faulty. So to check how significantly a variable causes other variables we will run this test with Ho as: X do not Granger-cause Y.

The results indicate that we can reject Ho and conclude that GDP does have some effect on GDPI, EX and IM, which we can interpret logically as well. In this way we should also check for other variables as well. Please try them out. For more information regarding this test please check out this link.
Forecasting:
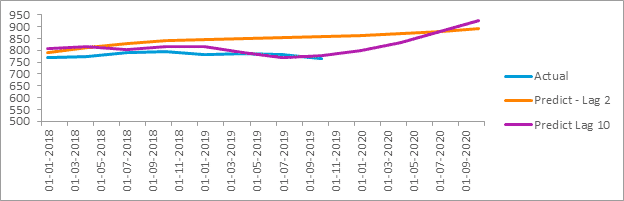
Finally, after all the checks we move on to forecasting. For checking which model is better fit the actual model we will forecast with both the lag 2 and 10 and plot them against one another. As you are aware that we have taken the data till 2017 for multi-variate time series modelling and left 2 years of data for comparison:
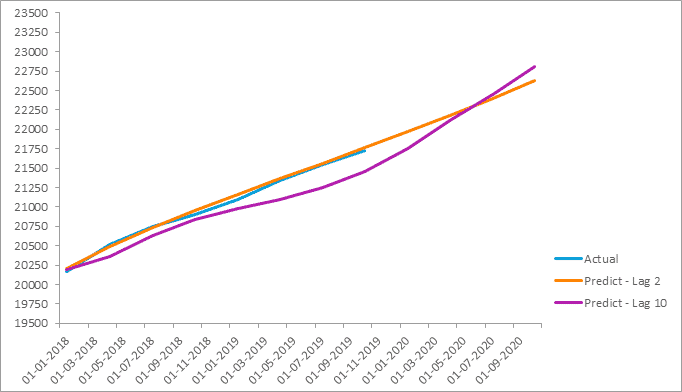
If we look the results for GDP, we can observe that with Lag 2 the model is pretty accurate. With Lag 10 there seems to be abnormal dip in the years of 2019 which is not in line with the actual data. You can also try by taking different lags and comparing them with the actual results to see which lag provides the good results.
We also have predictions for other variables:
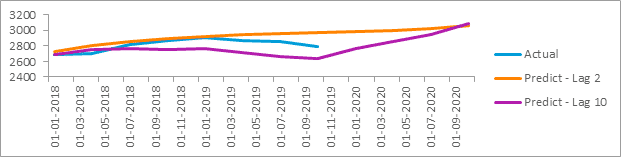
- Gross Domestic Private Investment (GDPI):
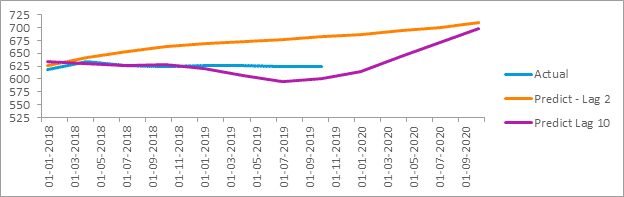
- Exports (EX):
- Imports (IM):
We can observe that for other variables the predictions with Lag 2 are not as satisfactory as for GDP. Hence, you could try running with different lags to improve the results or else you can also try running other time series models (like ARIMA, AR, ARCH) on them.
Also Read: Actuarial Time Series Modelling on Delhi’s Pollution (PM2.5) Levels
Ending Thoughts
This was all about Multi-variate time series modelling (VAR) in R. For more information on the dataset and codes for this model please feel free to reach out to me. Also, if you feel like having more variables/data in the model for better predictions please check out the link for acquiring data which is mentioned under “Data Description”. You could try running a multi-variate linear regression as well with this data and try to compare which model is better. Any views, suggestions or queries are welcomed.
This blog has been written by Yash Agarwal. I thank him for writing such a great blog and giving us permission to post it here. I urge you to visit his Linkedin profile and share your views/ideas/comments/feedback with him. Thanks for reading.
And, this article has been published here by Shivang Gumber.
.

