Quarantine has hit all of us hard. But it can be an opportunity in disguise. I thought to utilize my quarantine time for some productive purpose and bring my knowledge of actuarial subjects to practical use. But I wasn’t very sure of how to do it. I had studied Time Series ARIMA modelling recently while preparing for my CS2 exam. Well, I have been living in Delhi for the past 3 years for my graduation and hence thought why can’t it be a model on Delhi’s Pollution Levels throughout the year. Delhi’s pollution levels follow a seasonal pattern. It goes up during the months of Nov – Jan while falls during summers. This seemed an ideal dataset to model.
If anyone of you in knowing the in-depth details of the project, I’ll be more than happy to share the R file and the data with you. Feel free to message me on LinkedIn.
It was Arpit who motivated me and gave me the idea to construct a time series model on real-life data. Tamanna guided me throughout the process with the technicalities and the result was this beautiful thing. This wouldn’t have been possible without their support. So, a very special thanks to both of them.
Data Collection
I wandered from one website to another in search of a clean dataset. But that was not going to happen, especially in the case of India. Finally, I stopped at aqicn.org which has data for pollution parameters of past 7 years. This website, in turn, collects data from the website of the Central Pollution Control Board. I downloaded the data from the Punjabi Bagh monitoring centre as a CSV file. The data was from 1st Jan 2014 to 27th March 2020. I decided to model only one pollutant PM2.5 which is a major pollutant. The data was not weekly as I desired and hence, the next step in modelling, be it time series or of some other form is data cleaning.
Data Cleaning
I realized that not only the format wasn’t as desired but it also had missing values! I decided to fill in the data values from other monitoring stations in Delhi. But even after filling in the data it still had some missing values. For this I filled in the average of adjacent values.
Next, I took out the weekly averages of the daily data. My data was finally clean and ready to use. All of the data cleaning was done in Ms Excel using VBA since it was not possible to do all this on data with 2000+ rows. Also, a lot of errors could creep in and could take up a lot of time. Even after doing it with VBA, data cleaning part took me longest. The data of 2020 was deliberately not used in order to check the accuracy of the time series model. Finally, the line plot of data from Jan 2014 to Dec 2019 looked like this-
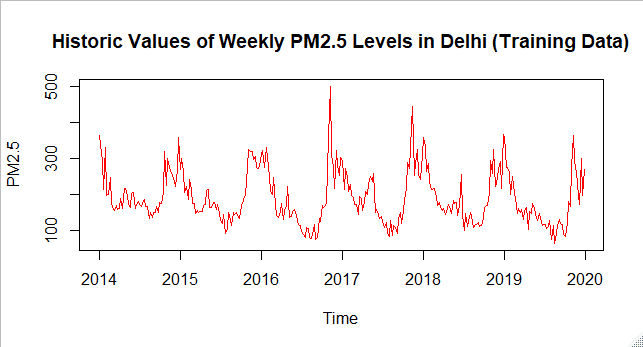
The plot was coherent with the seasonal nature of the pollution levels. It had it’s peaks in the winter months while it dropped in the summers. The next step was to analyze the data.
Analyzing Data
After realizing that analyzing the data was easier in R Language ,I switched to it. I imported the data using the “read_xlsx()” function from the “readxl” package. Being was familiar with the plot of the data and I knew that the data has seasonality. I analyzed the data by following these steps.
Differencing
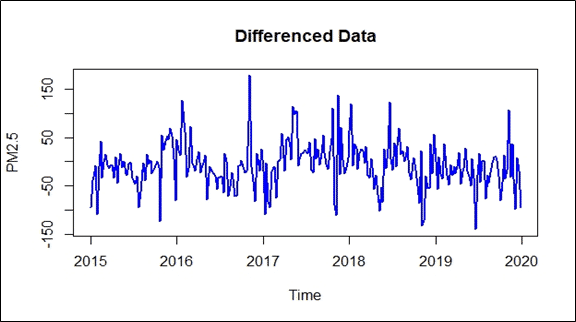
The first step I followed was to difference the data with lag 52 (pertains to 52 weeks) to remove the seasonality. The function I used here was “diff()”.
I plotted the differenced data and it looked like this.
Checking Stationarity
The data has to be stationary for any time series analysis. The plot looked promising, however, I decided to apply a formal test to check it. I used the Phillips-Perron test for checking stationarity of the data. Function used was “PP.test”.
The test returned the value 0.01 which was sufficient to reject the hypothesis that the data is not stationary. R gives us the following output.

Analyzing ACF and PACF
Analyzing Auto Correlation Function and Partial Auto Correlation Function is important to get insights about the data. It gives an idea about the values of p and q (the no. of parameters) to be used. The ACF came out to be decaying rapidly. While the PACF cut-off after lag 3. This suggested it to be an ARMA (3,0).
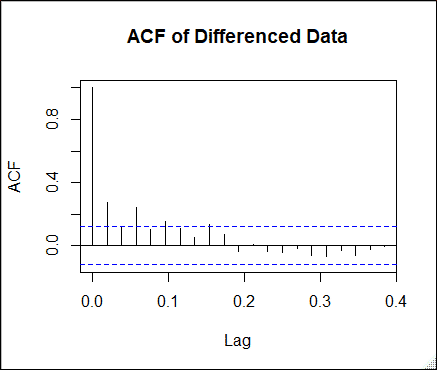
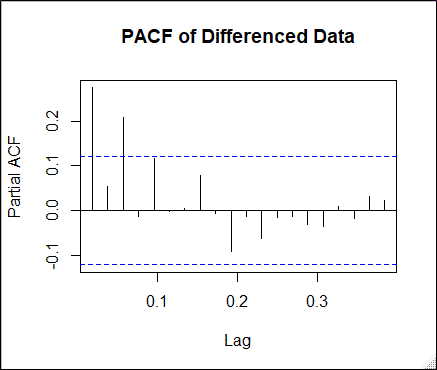
Fitting the Model
The next step was to fit a model to the data. I used “ARIMA ()” function for the job. I used p =3, d=0, q=0 initially. Note that this model is not fitted on the original data but on the data after seasonal differencing. Thus, this time series model will predict the seasonal differences. Here is the output of the code.

Thus our final equation becomes-
Xt = -7.9409 + .2545*Xt-1 – 0.0011*Xt-2 +0.2122*Xt-3 + et
The sigma^2 = 1991 represents the estimated variance of residuals or the error terms. The numbers below the estimated coefficients are the estimated standard errors of the coefficients. They can be used to find out Confidence Intervals of our predictions. We will know what AIC means when we compare this model to other models.
Analyzing Errors
It is assumed that the errors follow a N (0, sigma^2) distribution. Also, the errors must not be related to each other (no autocorrelation). In other words, the error is a white noise process. To check this, I plotted ACF of error terms. The plot suggested there was no autocorrelation among the errors as ACF cut-off after lag 0 (the blue line represents 95% CI around 0). Also, the error moved around 0 with almost equal variance.
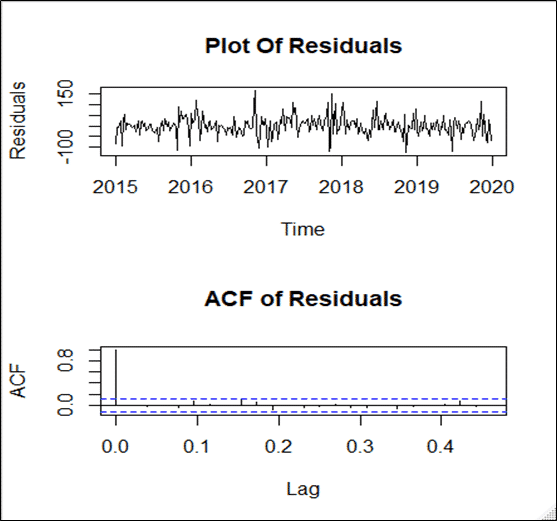
To check if this assumption formally we apply the Ljung Box test. I used the “Box.test()” function to carry out this test. Our time series model passed this test. I received the following output.

Thus, we have
ei ~ N (0, 44.622)
Predicting Values using Time Series model
It was now time to predict future values using the time series model we just prepared. I used the “predict ()” function to predict the values for the year 2020 (next 52 values). As noted earlier, these are the predictions of the future differences and the actual values. We need to add these differences to the corresponding original values from the year 2019. This was done using a for loop (there may be faster and easier ways to do that) looping over the 52 predictions. Finally, our predictions were ready. The plot came out to be like this.
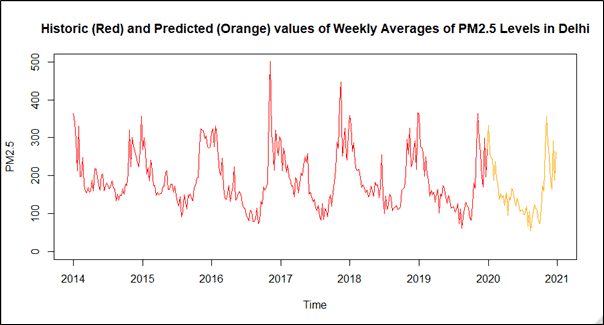
Comparing Predictions with Original Data and Other Time Series Models
Remember we did not use the data of the first 10 weeks of 2020 knowingly. It was time to bring that into use. We now plot the predicted data and the original data of 2020 to see how good our model fits.
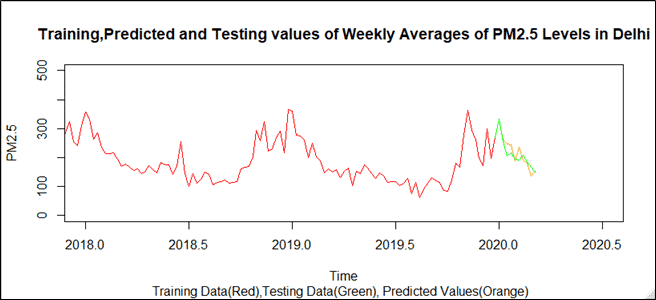
The data makes pretty good predictions especially at the start (notice how the original and the predicted values almost overlap). But how do we know that we have set the best values of p,q and d? To test this I analyzed the AIC, MAPE and RMSE from different models fitted on the same data. The summary table came out to be as below-
| ARIMA (3,0,0) with Seasonal Differencing | ARIMA (3,0,1) with Seasonal Differencing | ARIMA (3,1,1) after Seasonal Differencing | |
| AIC | 2723.17 | 2724.66 | 2718.03 |
| MAPE | 9.46% | 9.81% | 25.70% |
| RMSE | 24.64782 | 25.0013 | 51.69144 |
This table suggests that the time series ARIMA (3,0,0) predicts the most accurate results when different models were compared to the original data and errors were analyzed. This is evident from the values of AIC, MAPE and RMSE which are lowest for ARIMA (3,0,0). Thus, it is evident from the above table that our choice of fitting ARIMA (3,0,0) to the differenced data was correct. Further studies can be carried out with this model by constructing confidence intervals of predictions and by running simulations.
Make sure you try some of these by yourself. Your views, suggestions or queries are welcomed in the comment box.

