Continuous Distributions in Actuarial Applications

Actuarial Applications involve usage of probability distributions to a great extent. There are two types of probability distributions, one is Discrete Distributions and the other is Continuous Distributions.

Lets have a look to a few Continuous Distributions used in Actuarial Applications.

We will discuss the following Continuous Distributions here:

• Continuous Uniform Distribution
• Normal Distribution
• Gamma Distribution
• Exponential Distribution
• Lognormal Distribution

Continuous Uniform Distribution (rectangular Distribution)

A random variable X is said to follow a Uniform distribution over an interval (a, b) if its pdf is constant over the entire range of X.

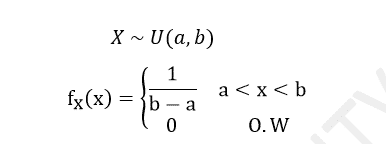
Mean:                                                                         

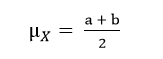
Variance:                                                                           

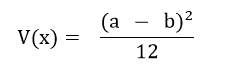
CDF:                                                                    

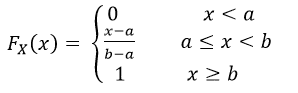
Applications:

The meaning of Uniform Distribution is the Random variable is equally probable (with probability) everywhere within the given range (a, b).

1. Like in a sequence of random numbers each and every Number is equally probable over the whole range of random numbers. This Uniformity property is the most important property to check the randomness of a sequence of random numbers.
2. In cricket, the probability that a batsman will hit a six in any of the balls in an over is equally probable.

Let, 

X=A random variable denoting the ball number in which a batsman hits a six  

Then, (Though it is hypothetical)

Application in R:

Suppose you want to simulate 10 values from a uniform(0,100) distribution

Code:

runif(10,0,100) ## This code will simulate 10 random values from U(0,100) Distribution

punif(20,0,100)-punif(10,0,100) 
## This code will give us the probability of getting a number between 10 to 20, that is, p(10<x<20).

x<-0:100
pdf<-dunif(x,0,100)
plot(x,pdf)
 ## this codes will give us the plot of the uniform distribution. The probability will remain constant across all values of x. The graph will be a straight line as shown below.

Output:

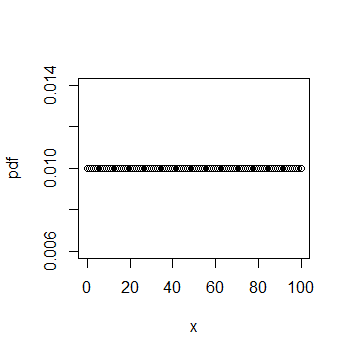
Normal or Gaussian Distribution

A Random variable X is said to follow a Normal or Gaussian distribution if its pdf is defined by:

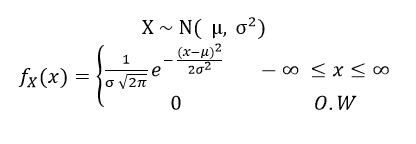
Mean(=median=mode):          

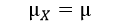
Variance:                                       

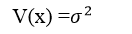
Standard Normal Distribution:

When we set µ=0 and σ=1 the Normal distribution becomes a Standard Normal distribution.

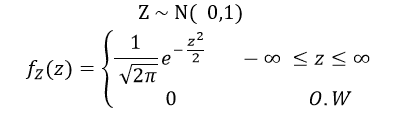
 Mean(=median=mode):          

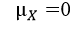
Variance:                                       

Var(x) =1

Applications:

Normal distribution is the most widely used distribution in Real life due to Central Limit Theorem. (According to Large Sample theory, every distribution approximately follows a Normal distribution when the sample is sufficiently large.)

1. Let, the owner of a nail producing factory wants to know the average length(cm) of a nail produced during a shift to set the Quality assurance parameters.

So, we collect the data of more than 80 to 100 nails produced during the shift randomly and then find its mean (let µ_n) and standard deviation (let σ_n )

Let X_n be a random variable denoting the average length of a nail (cm) 

From Large sample theory and CLT we can say that,

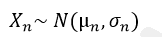
From here he can find out the Confidence interval of sample mean to know the range of the sample mean within which it lies.

• Traders may plot price points over time to fit recent price action into a normal distribution. The further price action moves from the mean, in this case, the more likelihood that an asset is being over or undervalued. Traders can use the standard deviations to suggest potential trades. This type of trading is generally done on very short time frames as larger timescales make it much harder to pick entry and exit points.

Application in R:

Suppose you want to simulate 10 values from a normal distribution with mean 5 and variance 9.

Code:

rnorm(10,5,3) ## please not that  parameters in R for normal distribution is mean and standard deviation. This code will simulate 10 values.
qnorm(0.8,5,3) ## This code will give us the 80th percentile of the normal distribution.

Gamma distribution

A random variable X is said to have Gamma Distribution if it has the following pdf:

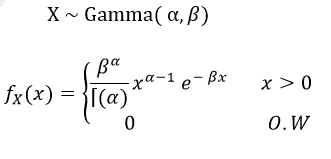
  where α>0 , β>0

Here, is the gamma function.

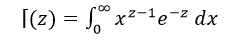
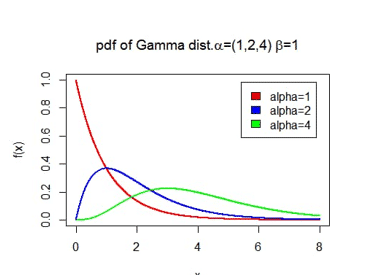
Mean:     

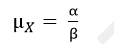
Variance:     

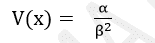
CDF:        

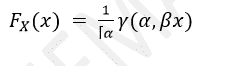
Applications

The gamma distribution can be used in a range of disciplines including queuing models, climatology, and financial services. For example, the events that may be modeled by gamma distribution include:

• The amount of rainfall accumulated in a reservoir
• The size of loan defaults or aggregate insurance claims
• The flow of items through manufacturing and distribution processes
• The load on web servers

Suppose that you are Goalkeeper of a football team and you expect to get a shot on goal once in every 5 Minutes. Compute the probability that you will have to wait between 2 to 4 min before you get next shot on goal. One shot every 5 minutes means we would expect to get 1/β= 1/5 shot every minute on average. Using β = 5 and α =1 we can compute this as follows:

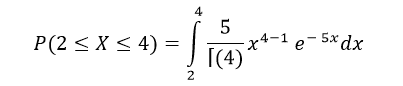
The computation in R can be done in the similar way as for other distributions with parameters being β & α. The codes are:

rgamma(n, α, β) ## to simulate n values with parameters β & α.
qgamma- to get the qth percentile
dgamma- to get the PDF
pgamma- to get the CDF

Exponential distribution

A special case of Gamma distribution (when α=1) is Exponential distribution. So, its pdf is denoted by-

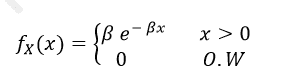
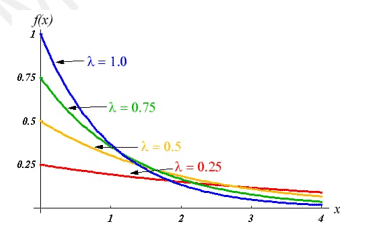
Mean:             

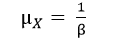
Variance:         

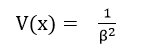
CDF:        

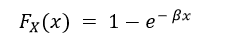
Applications in R:

In general, the waiting time of a Poisson process is said to follow Exponential Distribution.

If the number of claims in General Insurance company follows Poisson distribution with Lamda = 5 claims per day. What is the probability that the next claim occurs in less than 3 hour.

ANSWER:  Since the time between 2 claims is Exponentially distributed with parameter λ, the probability would be:

P(X<t₀) =1 − exp (−λt₀)

Code in R:

The average number of claims in a day is 5, so in an hour it will be 5/24.

pexp(3,5/24) ##this code will give us a probability of getting a claim in less than 3 hours.

Lognormal Distribution

A continuous distribution in which the Logarithm of a variable has a Normal Distribution is said to be Lognormal Distribution.

Log(X) ~ Normal Distribution, 

Therefore, X ~ Lognormal Distribution with parameter µ and σ².

The PDF of the lognormal distribution is given by-

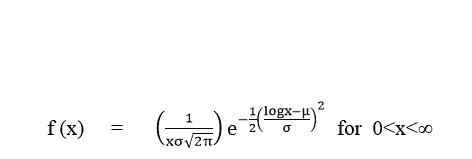
Mean:             

            

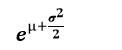
Variance:         

Applications:

1. It is a positively skewed distribution which can be widely used to model claims losses in insurance industries or Loan defaults in Banks.
2. A log normal distribution results if the variable is the product of a large number of independent, identically-distributed variables in the same way that a normal distribution results if the variable is the sum of a large number of independent, identically-distributed variables. So, this is equivalent to Normal approximation using the Central limit theorem.
3. The variates, for instance like the size of silver particles in a photographic emulsion, the survival time of bacteria in disinfectants, the weight, and blood pressure of humans are Log normal variates.

Computation in R-software:

Please note that the parameter in R will be  

rlnorm(n,  ## it will simulate n-values from the Lognormal distribution with the parameter

rlnorm(n, μ,σ) ## it will simulate n-values from the Lognormal distribution with the parameter μ and σ

Similarly we can use the following codes to compute:

dlnorm-to compute the PDF
qlnorm-to compute the Percentile
plnorm- to compute the CDF

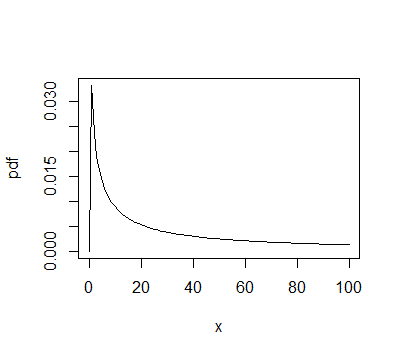
Code to Plot the Lognormal Distribution in R-software:

## plotting Lnorm(5,9) Distribution in R-software:

x = 0:100
pdf =dlnorm(x,5,3)  
plot(x,pdf,type="l")

Output:

Please note that the meaning of r, p, d & q is the same for all the distributions.

With the help these Continuous Distributions we can apply them in a wide range of actuarial areas.

This article was written by Shreyansh Agarwal and Kountenyo Roy Chowdhury. We urge you to share your views and feedback with them.

This article is published by Jinal Shah.