How convexity and duration are used to solve real business problems. But before moving to that let’s first understand what convexity and duration actually is!
Duration (or modified duration) is a linear measure (or 1st derivative) of how the price of a bond changes in response to interest rate changes. In general, the higher the duration, the more sensitive the bond price is to the change in interest rates. Duration of a bond is the linear relationship between the bond price and interest rates. As interest rates increase, bond price decreases( remember equation of value’s relation between bond price and interest as bond price is present value of all the future coupon payments and final redemption payment.)
More relatable and prudential reason for inverse relationship between bond price and interest rates is explained with an example:
Suppose :
If an investor owns a fixed interest bond that pays 5% and interest rates begin to rise above 5% in that market, then the investor may want to sell this lower paying security. The reason for the sell-off is that their existing bond’s interest rate is less attractive than the current market rate. Investors don’t want to hold a bond that pays 5% if they can invest the same principle into one that pays a higher rate of interest in the future. In a rising rate market, bondholders look to sell their existing bonds and opt for newly-issued bonds paying higher yields.
Because there is an abundance of bonds at the lower rate on the market, the prices for these debt holdings will drop. As a result, bond prices and yields move in the opposite or inverse directions.
Simply put, a higher duration implies that the bond price is more sensitive to rate changes. For a small and sudden change in bond yield, duration is a good measure of the sensitivity of the bond price i.e. its change as a result of that interest rate change because for very small changes it is prudent to assume that the change in price and change in interest are correlated linearly.
However, for larger changes in yield, the duration measure is not effective for telling the sensitivity of bond prices as the relationship is non-linear and is a curve. As interest rates change, the price is not likely to change linearly, but instead it would change over some curved function of interest rates. The more curved the price function of the bond is, the more inaccurate duration is as a measure of the interest rate sensitivity.
Here is when convexity comes into picture! Convexity is a good measure for bond price changes with greater fluctuations in the interest rates. Mathematically speaking, convexity is the second derivative of the formula for change in bond prices with a change in interest rates and a first derivative of the duration equation. Don’t worry if the last line didn’t make sense- you just have to understand it and not cram it.
Derivative of price with respect to interest rate is duration – The first derivative!
Derivative of duration with respect to interest rate is Convexity – the second derivative of price with respect to interest rate !
Makes a little sense now?
It will make much more… Read on!
Convexity is a measure of how the duration of a bond changes as the interest rate changes. Convexity measures the curvature in this relationship i.e. how the duration changes with a change in yield of the bond.
Convexity is a risk management tool used to define how risky a bond is as more the convexity of the bond, more is its price sensitivity to interest rate movements. A bond with a higher convexity has larger price change when the interest rate drops than a bond with lower convexity.
Geometrically, when the model showing the relationship between two variables(say the price of the bond and the interest rates) is not flat but curved, the degree of curvature is called the convexity – see picture below!
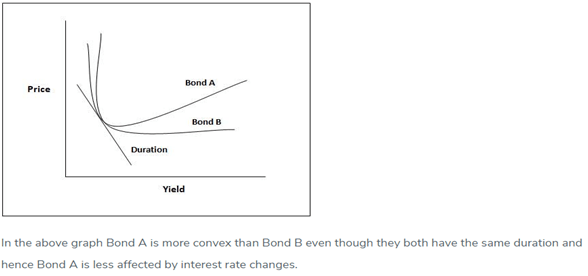
Significance of convexity and duration in real life:
Hence when two similar bonds are evaluated for investment with similar yield and duration the one with higher convexity is preferred in a stable or falling interest rate scenarios as price change is larger. In a falling interest rate scenario again a higher convexity would be better as the price loss for an increase in interest rates would be smaller.
So , more the convexity, lesser is the effect of interest rates on change in prices of a bond ! Why?
Bonds with greater convexity (or curvature) are more prone to gain in price when yields fall and price falls less when yields rise. So it is best suited to consider bond with higher convexity for overall stability of the market.
Types of convexity:
Convexity can be positive or negative. A bond has positive convexity if the yield and the duration of the bond increase or decrease together, i.e. they have a positive correlation. This typical is for a bond which does not have a call option or a prepayment option. Bonds have negative convexity when the yield increases and the duration decreases i.e. there is a negative correlation between yield and duration. These are typically bonds with call options, mortgage-backed securities and those bonds which have a repayment option. If the bond with prepayment or call option has a premium to be paid for the early exit then the convexity may turn positive.
Factors affecting convexity:
The coupon payments and the periodicity of the payments of the bond contribute to the convexity of the bond. If there are more periodic coupon payments over the life of the bond then the convexity is higher making it more immune to interest rate risks as the periodic payments help in negating the effect of the change in the market interest rates. If there is a lump sum payment then the convexity is the least making it a more risky investment.
Also Read: Indian Insurance Sector – At the Crossroad of Development

