This post is by Mathematicacity. The link to the website is given below. https://mathematicacity.co.in
Meaning of Reinsurance: Reinsurance is the insurance taken by the insurance companies itself. The reinsurance is undertaken by the insurance companies to mitigate risk. It helps the company to share the burden of risk with the reinsurance company. There is no contact between the reinsurance company and the client. The insurance company acts as middle man.
In this article we will only explain about the two most common types of reinsurance arrangement- Quota share (proportional reinsurance) & Excess of loss (Non-proportional)
Types of Reinsurance: Generally the reinsurance contract is of two types-
- Proportional reinsurance: Under proportional reinsurance, the insurer and reinsurer share a pre-decided proportion of each claim. For example, suppose for a particular motor insurance, the insurer might agree to pay 80% of each claim and the rest 20% being paid by the reinsurer. Under this arrangement, both insurer and reinsurer are involved in the payment of each and every claim.
This type of proportional reinsurance agreement is also known as quota share reinsurance. The proportion of payment by reinsurer and insurer remains constant for each and every claim.
For example:
Suppose a motor insurance policy gave rise to 3 claims in a year of amounts 1200, 1000 and 1500 respectively.
The quota share of insurer is 80% and reinsurer is 20%.
Payments by insurer – 960, 800 & 1200 respectively
Payments by reinsurer- 240, 200 & 300 respectively
The chart below shows the payment made by insurer and reinsurer for each of the 3 claims. We can clearly see that both insurer and reinsurer are involved in the payment of each and every claim.
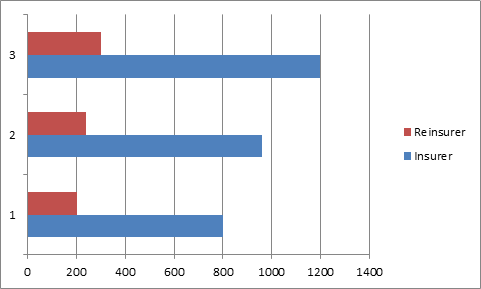
The horizontal axis indicates claim amounts and the vertical axis denotes claim number.
- Non-proportional reinsurance: Under non-proportional insurer, the reinsurer is not involved in the payment of each and every claim. Under this arrangement, the reinsurer is involved only in those claims which falls in a certain layer or exceeds a certain pre-decided threshold. The layer is defined by a lower limit and an upper limit.
The excess of loss (XOL) reinsurance is the most common type of non-proportional reinsurance arrangement. Under XOL reinsurance, the reinsurer is involved only in those claims that exceed a certain retention limit. The reinsurer pays only that part of
claim amount which exceeds the pre-decided retention limit.
For example:
Suppose a motor insurance policy gave rise to 3 claims in a year of amounts 1200, 1000 and 1500 respectively.
The reinsurance arrangement is XOL with retention limit = 1100
Payments by insurer- 1100, 1000, 1100
Payments by reinsurer- 100, 0, 400
The chart below shows the share of payment by both insurer and reinsurer for all the claims. We can see that the reinsurer is not involved in the payment of all the claims, unlike in proportional reinsurance.
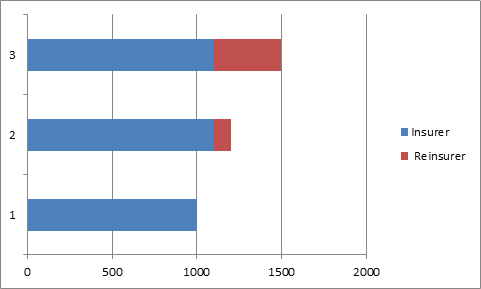
The horizontal axis indicates claim amounts and the vertical axis denotes claim number.
Application of Reinsurance in R-Software:
- Proportional Reinsurance (Quota share) –
Suppose the claims distribution is modelled using exponential distribution with parameter Lamda = 0.01. The total number of claims expected is 500 (say).
The insurer quota is 80% and the reinsurer quota is 20% of each claim
Code –
n=500 ##since the expected number of claims is 500
lamda=0.01 ##storing the parameter of the exponential distribution
x=rexp(n,lamda) ##simulating the amount of each of the 500 claims using the exponential distribution
y=0.8*x ##storing the amount to be paid by the insurer in the variable y
z=0.2*x ##storing the amount the reinsurer is liable to pay in the variable z
mean(x) ##this will give us the mean claim amount. This will vary a little from the theoretical mean of exponential distribution as we are simulating.
mean(y) ##this will give us the mean claim amount to be paid by the insurer
mean(z) ##this will give us the mean claim amount to be paid by the reinsurer
2. Non Proportional Reinsurance ( Excess of loss)-
Suppose the claims distribution is modelled using exponential distribution with parameter Lamda = 0.01. The total number of claims expected is 500 (say).
The retention limit is 140(say).
Code-
n=500
lamda=0.01
x=rexp(n,lamda)
Retention=140
y=pmin(x,Retention) ##this will give us the amount to be paid by the insurer for each and every claim
z=pmax(x-Retention,0) ##this will give us the amount to be paid by the reinsurer for each and every claim. For, most of the claims the reinsurer will not be involved in the payment of the claim and the amount paid will show 0 in output.
length(z[z>0]) ##this will give us the number of claims in which reinsurer is involved
z[z>0] ##this will give us the amount of each claim that is to be paid by the reinsurer
length(z[z>0])/length(z) ##this code will give us the Probability that a claim will involve a reinsurer.
Example-
Suppose the Number of claims from a motor insurance policy is 5 (hypothetical). The amount of each of the claim is to be hypothetically simulated using exponential distribution with parameter lamda=0.001.
The reinsurance arrangement is of excess of loss type. However, no specific retention limit has been decided yet. The one of the following retention limit is to be considered:-
1500, 1750, 2000, 2250, 2500 & 3000
Our task is to calculate the amount to be paid by the insurer and reinsurer under each of the given retention limit.
We also have to calculate the mean and variance of the claims for both reinsurer and insurer under each of the given retention limit.
We also have to show how the mean and variance of claims changes with retention limit for both insurer and reinsurer using diagrams.
Solution:-
retention=c(1500,1750,2000,2250,2500,3000) ##creating a vector of retention limit
set.seed(171) ## it is used just to fix the values of each simulation permanently.
x=rexp(5,0.0001) ## simulating values for all of the 5 claims
## calculating the share to be paid by the insurer under each retention limit
for(i in 1:6) {
insurer=pmin(x,retention[i])
print(insurer) }
## Calculating the amount to be paid by the reinsurer under each retention limit
for(i in 1:6) {
reinsurer=pmax(x-retention[i],0)
print(reinsurer) }
## Calculating the mean amount to be paid by the Insurer under each retention limit
for(j in 1:6) {
insurer=pmin(x,retention[j])
print(mean(insurer)) }
## Calculating the mean amount to be paid by the reinsurer under each retention limit
for(i in 1:6) {
reinsurer=pmax(x-retention[i],0)
print(mean(reinsurer) }
## Calculating the variance of the claims to be paid by the insurer under each retention limit
for(j in 1:6) {
insurer=pmin(x,retention[j])
print(var(insurer)) }
## Calculating the variance of the claims to be paid by the insurer under each retention limit
for(i in 1:6) {
reinsurer=pmax(x-retention[i],0)
print(var(reinsurer)) }
## Plot showing how the mean amount of the insurer will vary under each retention limit
Code:
meaninsurer=c(1364.279,1522.837,1672.837,1822.837,1972.837,2103.701 ) ## storing the mean amount calculated above in a vector
plot(retention,meaninsurer) ## plot of mean under each retention limit
Output:
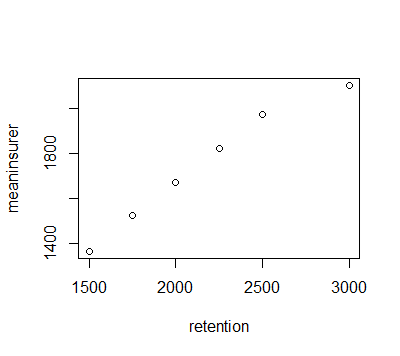
## We can see that as the retention level increases, the mean amount to be paid the insurer also increases
## Plot showing how the mean amount of the reinsurer will vary under each retention limit
Code
meanreinsurer=c(3531.515,3372.957, 3222.957,3072.957,2922.957,2792.093) ## creating a vector of mean amount to be paid by the reinsurer under each retention limit.
plot(retention,meanreinsurer) ## a plot showing the mean amount to be paid by the reinsurer under each retention limit
Output
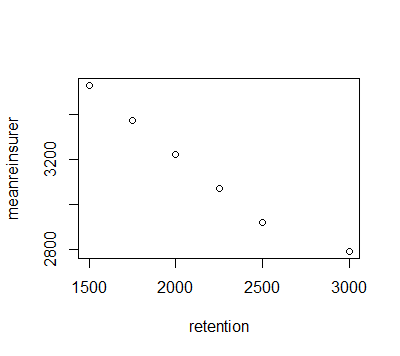
## We can see that the mean amount to be paid by the reinsurer deacreases as the retention limit increases(contrary to the insurer)
## Plot showing how the variance amount of the insurer will vary under each retention limit
Code
varinsurer=c(92100.42,161806.3,265742.4,407178.4,586114.4,804758.9) ##Storing the variance of claim of insurer under each retention limit in a vector
plot(retention,varinsurer) ## plotting the variance of insurer under each retention limit
Output
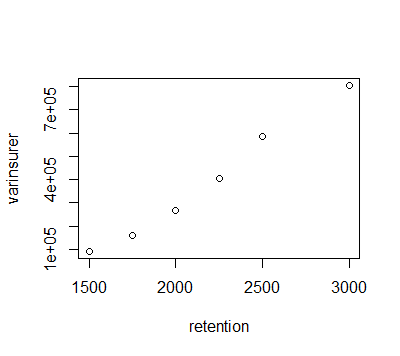
## We can see that the variance of the insurer increases with the increase in retention limit
## Plot showing how the variance amount of the reinsurer will vary under each retention limit
Code
varreinsurer=c(44749716,43962732,43138243,42351254,41601764,38978930)
plot(retention,varreinsurer)
Output
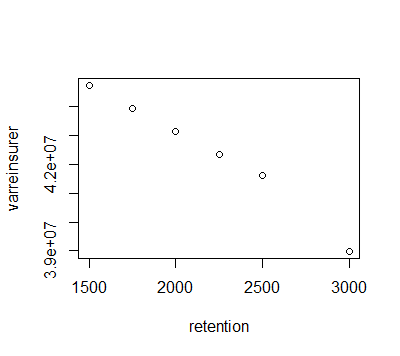
We can see that as the retention limit increases (all other thing being same), the mean and variance of claims to be paid by the insurer increases & the mean and variance of claims to be paid by the reinsurer decreases.
So we can say that the insurer should retain higher proportion of the premium as the retention level increases (all other things being constant).
Do subscribe the mailing list of Mathematicacity to get latest updates on R. Do not forget to confirm your subscription. The link to the website is given below:
Do reach out to us if you have any query. We hope this article will be helpful to you.
